Zadanie 3. Określenie parametrów orbity gwiazdy S2 oraz jej okresu obiegu
Posiadając podane poniżej współrzędne gwiazdy S2 w różnych czasach należy dopasować do niej elipsę. Elipsa ta będzie przybliżoną orbitą gwiazdy S2, a to dlatego że każdy z punktów posiada pewną niepewność pomiarową
| Data (rok) | Współrzędna x (arc sec) | Niepewność dx (arc sec) | Współrzędna y (arc sec) | Niepewność dy (arc sec) |
|---|---|---|---|---|
| 1992,226 | 0,104 | 0,003 | -0,166 | 0,004 |
| 1994,321 | 0,097 | 0,003 | -0,189 | 0,004 |
| 1995,531 | 0,087 | 0,002 | -0,192 | 0,003 |
| 1996,256 | 0,075 | 0,007 | -0,197 | 0,010 |
| 1996,428 | 0,077 | 0,002 | -0,193 | 0,003 |
| 1997,543 | 0,052 | 0,004 | -0,183 | 0,006 |
| 1998,365 | 0,036 | 0,001 | -0,167 | 0,002 |
| 1999,465 | 0,022 | 0,004 | -0,156 | 0,006 |
| 2000,474 | -0,000 | 0,002 | -0,103 | 0,003 |
| 2000,523 | -0,013 | 0,003 | -0,113 | 0,004 |
| 2001,502 | -0,026 | 0,002 | -0,068 | 0,003 |
| 2002,252 | -0,013 | 0,005 | 0,003 | 0,007 |
| 2002,334 | -0,007 | 0,003 | 0,016 | 0,004 |
| 2002,408 | 0,009 | 0,003 | 0,023 | 0,005 |
| 2002,575 | 0,032 | 0,002 | 0,016 | 0,003 |
| 2002,650 | 0,037 | 0,002 | 0,009 | 0,003 |
| 2003,214 | 0,072 | 0,001 | -0,024 | 0,002 |
| 2003,353 | 0,077 | 0,002 | -0,030 | 0,002 |
| 2003,454 | 0,081 | 0,002 | -0,036 | 0,002 |
Tabela 1. Współrzędne gwiazdy S2
Aby opisać dowolną elipsę należy dokonać jej obrotu i przesunięcia. Problem ten można rozwiązać korzystając z macierzy i równań opartych na współrzędnych biegunowych.
Każdy punkt elipsy we współrzędnych biegunowych można zapisać jako:
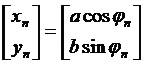
gdzie:
a - wielka półoś orbity
b - mała półoś orbity
fin - kąt biegunowy (0 - 2pi)
Te współrzędne opisują nam punkty elipsy nie obróconej pod żadnym kątem o środku w punkcie (0;0).
Kolejny wzór przedstawia macierz obrotu o kąt alfa:
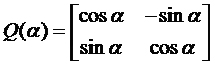
Dzięki macierzy obrotu możemy wyliczyć współrzędne każdego punktu elipsy obróconej pod pewnym kątem. Współrzędne te możemy obliczyć w następujący sposób:
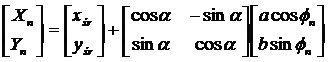
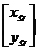to współrzędne środka elipsy
Ostateczne wzory, które będą nam potrzebne to:
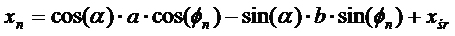
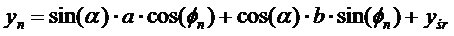
Aby wyliczyć okres obiegu należy policzyć pola trójkątów, których wierzchołki składają się z dwóch kolejnych
punktów i ogniska. Pole to możemy wyliczyć ze wzoru:
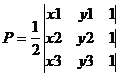
Jak wiemy z II prawa Keplera ciało niebieskie zakreśla takie samo pole w równych odstępach czasu.
Potrzebne do tego będzie jeszcze pole elipsy, które można obliczyć ze wzoru:
P = pi*a*b
Powyższe ćwiczenie możemy rozwiązać z wykorzystaniem arkusza Excela, co przedstawione zostanie w kolejnym punkcie.
